
3. 범주 → 범주
1) 교차표 작성
- 가장 먼저 실행해야 할 것은 교차표 작성이다.
- 교차표는 crosstab함수로 가능하다!
pd.crosstab(행, 열, normalize='columns | index | all')→ columns = 열기준 | index = 행기준 | all = 전체 기준
2) 시각화
a. 모자이크 플롯(mosaic plot)
- mosaic plot은 범주별 양과 비율을 그래프로 나타내 준다.
mosaic(df, [행, 열])

- x축 길이는 각 객실등급별 승객비율 그 중 3등급 객실을 보면, y축 길이는 3등급 객실 승객 중 사망/생존 비율 각각의 면적은 전체에서 그 칸이 차지하는 비율
- 빨간선은 생존에 관한 전체 평균을 의미함 많이 떨어질수록 더 의미가 있다(?)
- 두 범주형 변수가 아무런 상관이 없으면 범주 별 비율 차이가 전혀 없다. → 조금이라도 관련 있으면 비율, bar 크기에 조금이라도 차이가 있다

3) 수치화
a. 카이제곱검정
- 기대빈도 : 아무런 관련이 없을 때 나올 수 있는 빈도 수(빨간 네모)
- 실제 데이터 : 관측된 값들(파란네모)
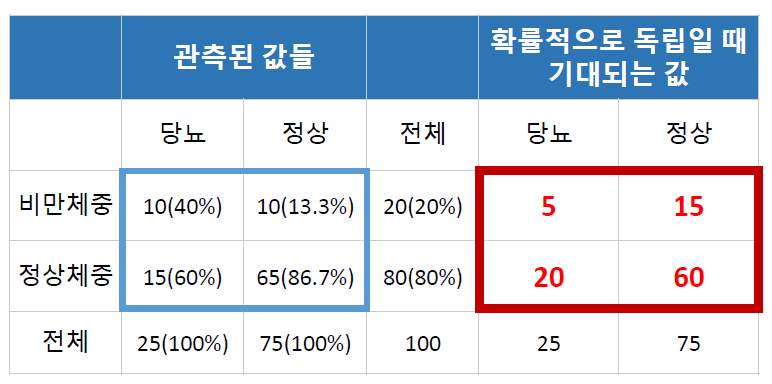
- 카이제곱 통계량 = 기대빈도와 실제 데이터의 차이!!
- 클수록 기대빈도로부터 실제 값에 차이가 크다
- 범주의 수가 늘어날 수록 값은 커지게 되어 있음
- 자유도의 약 2배 보다 크면, 차이가 있다고 본다. 자유도 = 범주의 수 -1 카이검정 자유도 = (x 변수의 자유도) * (y 변수의 자유도)
- 자유도에 대한 이해 → 예를 들어서 0,1로 무엇을 정하기로 했는데, 남자를 0으로 하면 여자를 1로 저절로 지정됨. → 즉, 1개만 정하면 나머진 저절로야~ 이러면 자유도 1이 되는 것!
- #먼저 교차표집계
table = pd.crosstab(행, 열) -> 하지만 nomalize는 없어야함#카이제곱 검정spst.chi2_contingency(table)
- 결과 → 카이제곱 통계량 → p-value → 자유도 : 행 자유도 * 열 자유도 → 기대빈도 : 계산된 값

4. 숫자 → 범주
1. 시각화
hist도 fill 옵션을 주고 보면 좋을 것이다!!!!
kde는 무조건 옵션 False 주고 해야한다!!!!!
a. kde plot


